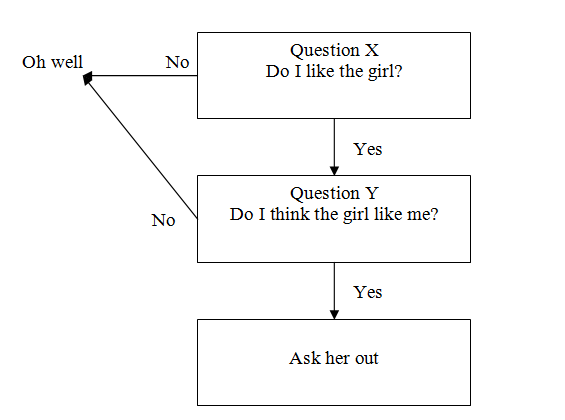
|
It is a truth universally acknowledged that a man wearing cute socks must be in search of a wife. The other day, what should crop up of facebook but a link to a blog post the title of which went something like: "Why aren't men asking woman out any more?" I didn't read it, in my defence, I don't have to. The blog will contain some mediocre application of some Bible verses lifted out of context, a lot of complaining about men not being brave enough, modern culture ruining good old fashioned courtship and more than it's fair share of spurious nonsense coached in spiritual language. I may just have described my own blog there... Either way, the blog post was hardly what I would call a definite answer on the subject. No, for such profundity, please read on. Men are, after all, simple creatures and it should be down right easy to model their thought processes. A man will ask a woman out based on the following flowchart: Simple. This can even been represented as a mathematical relationship. Call the first question X and the second Y. Assign each a binary value: 0 for no and 1 for yes. If X + Y = 2 a man will ask the girl in question out. If the answer is less than 2 no such request will be forthcoming. At this point objection made be raised that representing the vagaries of love with maths is reductionist in the extreme. But I'm an economist and diminishing a man to a maths equation is all they taught me at university.
Obviously, there is also a deviant equation where the woman asks the man out but that's not the question under discussion. Presumably, there exists a mathematical equation complicated enough to map the mysterious maze of the mind of a woman but it hasn't been invented yet. This is meant as a half hearted compliment. We'll restrain ourselves to the investigation of the male mind, it tends to operate on a more basic level. In saying that, our first equation, while at first glance a definitive answer to the posed question, is sadly flawed. For while these two questions much be answered then each man will have a bias towards favouring either question X or question Y. For example, there are men for whom the first question is almost everything and likewise, there are other men for whom, even if their heart was totally enraptured with a woman, would never ask her out if they thought the answer to the second question was within a remote chance of being a no. Once again, we can represent this mathematically, a man will ask a girl out when: (B1 + X) + (B2 + Y) = 2; where B1 + B2 = 1. Thus, if a man is only concerned with his own feelings: B1 equals 1 and B2 equals 0 and he likes her but thinks she doesn't like him, the equation reads: (1+1)+(0+0)=2. Most of us either know someone like this or have been there ourselves. Unfortunately, this equation does not quite hold true for if a man is only concerned with whether a girl likes him (B2 = 1) and he doesn't think she does (Y=0) despite the fact he likes her (X=1) for we get: (0+1)+(1+0) = 2. This is a false result, for logically, it doesn't hold that he would ask her out. Also, (1+0)+(0+1) is a similarly illogical result. Therefore, we have to rewrite the equation as: (B1 + X)B1 + (B2 + Y)X. This way, if the above situation occurs we get: (0+1)x0 + (1+0)1 = 1. No asking out, as we would expect. If question X is answered no, the maximum value of the equation is 1 (if B1 = 1) below our limit of 2. At this point, you might point out that this weights the first question too much but unless the first question is answered yes a man will rarely trouble to ask the second question. You could argue that the one exception to the above equation is the well known phenomenon of a guy beginning a romantic endeavour purely based on her feelings and not his. Yet in this case, the man thinking the girl likes him (Y=1) will then cause X to equal 1 and the equation holds. Our equation holds true for extremes but what about the moderate? Let us say a man holds both questions as having equal worth. B1 and B2 both equal 0.5. If he likes a girl we get (0.5 +1)x0.5 for the first half of the equation resulting in a value of 0.75. If he dislikes a girl the value is (0.5+0)x0.5=0.25. Now for the other side: if he thinks she likes him: (0.5+1)1 = 1.5. And if he thinks she doesn't: (0.5+0)1 =0.5. Bring those two sides together: if a man thinks they both like each other: 0.75+1.5=2.25. If he thinks they both don't 0.25+0 = 0.25. Even better if he does and she doesn't: 0.75+0.5=1.25 and he doesn't ask her out. And, of course, if he doesn't like her the whole thing equals 0. An excellent result all round if we modify our equation to (B1 + X)B1 + (B2 + Y)X >= 2. There may exist some other value for which the above equation would fail but having checked the extremes and checked the moderate position I am comfortable using this going forward. What have we learned so far? Mathematically, we have demonstrated that if (B1 + X)B1 + (B2 + Y)X >= 2 a man will ask a woman out. This is good going and we have already put 6000 years of the human history of romance and a hundred thousand books on love to shame. To think how many chick flicks would have been ended sooner if either of the two parties had access to the above equation! However, our equation is merely adequate for the representation of this complex socio-emotional issue. Put on your thinking cap, it's time to go a step further and add the fourth dimension. I am of course, talking about physical beauty. Ok, that was a joke. Physical beauty is assumed to factor into question X - whether a man likes a girl in the first place. The exact weighting it gets I leave to your own opinion. No, there is a time dimension to this equation, or rather, a timeliness dimension. Some men are good at both knowing what they feel and knowing what a woman is feeling. Some men are bad at these two things and take a long time to see what is often blatantly obvious to everyone else. Of course, to make matters more complicated, a man might be able to read women easily but struggle to make up his mind about his own feelings. Now, for this question of whether a man will ask a woman out I think we have to assume that un-timeliness is a negative. The longer it takes for a man to make up his mind the more chance the girl will find someone else or grow tired of waiting. Exceptionally slow men may even require a third party to intervene in order to prompt a decision. We'll call this new factor T, and it is the inverse of timeliness. That is to say, the more on the ball a man is with his feelings (and her feelings), the shorter the time period it takes to make up his mind, and the higher the value of T. Conversely, if it takes a man ages to work out if a girl likes him, T takes on a very small value. The application to this equation is obvious, a higher T means it is more likely for a man to ask a girl out. What we need to decide is its magnitude in the equation. Let's say that T can range from 0 to 2. And let's split it into TX and TY, each representing the respective timeliness. Then our equation becomes: ((B1 + TXX)B1 + (B2 + TYY)X) >= 2. Average timeliness (T=1) has no affect on the equation. In extreme cases (T=2), this can double the value of the answer yes while the opposite (T=0) has an extremely detrimental affect! Conversely, if the answer to a question is no, timeliness has no relevance, which is a tricky one. If a man doesn't like a woman might not that be caused by his excessive slowness to work things out? There could be a causal link between TX and X (and TY and Y). This might seem problematic but in reality, I think it still holds out. If a low TX increases the chance of X equalling 0 all we are saying is that a man who takes a long time to make up his mind will rarely answer the question: "Do I like this girl?" with yes. And that seems a sensible enough truth. So then ladies, next time you are worrying about some man whom you have set your heart on, not asking you out, bring the following equation to mind: ((B1 + TXX)B1 + (B2 + TYY)X) >= 2. Learn to love it's mathematical precision for it explains, in the simplest of terms, why you remain unpursued. Love, that great mystery beyond all mysteries, solved with a concentrated application of logic. You can thank me later.
0 Comments
Leave a Reply. |
Archives
October 2018
Categories
All
|